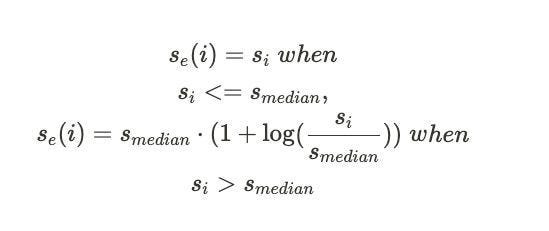Crafting Swift Consensus: The Journey to 1-Second Finality on Harmony

Abstract

As blockchain technology advances, there is a growing demand for enhanced transaction speeds and efficiency. The Harmony Protocol, a sharded blockchain built to promote the creation and use of decentralized applications (dApps), is pioneering in this area by implementing a 1-second finality. This study provides a comprehensive analysis of this monumental leap, signaling a significant progression in the blockchain realm.

The paper explores the prevalent challenges in the blockchain environment, presenting Harmony’s unique strategies to address these as part of Harmony Improvement Proposal 30 (HIP-30). With HIP-30’s substantial amendments, Harmony is on track to achieving 1-second finality. Our primary findings suggest that these enhancements will dramatically improve transaction times, addressing longstanding scalability concerns in the blockchain sector.

We further discuss the introduction of responsiveness into blockchain protocols, examining its importance and reviewing two significant protocols: PaLa and Simplex. We delve into how their techniques can be adapted for Harmony and the potential benefits and drawbacks this could entail.

Lastly, we offer an in-depth comparison of Harmony’s performance against traditional blockchains, focusing on dApp development, user adoption, and overall blockchain scalability. The paper concludes by emphasizing the importance of these innovations in shaping the future of blockchain technology, with implications for the Harmony Protocol and the broader blockchain community seeking to improve transaction efficiency and overall network performance.

Introduction

Blockchain technology has emerged as a pivotal innovation, paving the way for decentralized solutions in various industries. At the heart of this technology lies the principle of transaction finality — the guarantee that once a transaction has been included in the blockchain, it cannot be reversed or altered. This concept is paramount for any blockchain-based system, ensuring immutability and trust within the network. Nevertheless, achieving transaction finality has been challenging for many blockchain networks due to inherent constraints in decentralized system design and the trade-off between decentralization, security, and scalability. This paper aims to delve into the technical details and the innovative strides the Harmony protocol takes to enhance transaction finality time to a groundbreaking 1-second.

Since its inception, the Harmony protocol has been a forerunner in addressing the most pressing challenges in the blockchain ecosystem. Employing a sharded blockchain design and leveraging its unique Effective Proof-of-Stake (EPoS) consensus algorithm, Harmony has already achieved a remarkable 2-second transaction finality. This impressive feat was realized by minimizing the number of communication rounds during the consensus process, reducing the time needed to confirm each transaction.

In mathematical terms, we can express the transaction finality as a function of the number of communication rounds, n, and the time required for a round-trip message, t (assuming a fully connected network). This relationship can be expressed as:

F = n ⋅ t

Where F is the transaction finality time.

In Harmony’s current state with 2-second finality, we can see that ncommunication rounds and t time per round work together to achieve this. However, to further reduce this finality time to 1-second, Harmony is taking a significant leap by strategically reducing the n value (communication rounds), thus decreasing the F value (finality time) while maintaining the network’s security and decentralization.

As we delve further into the technical details, it will become evident how Harmony’s innovative approach solves one of blockchain technology’s key challenges and sets a new precedent for transaction speeds in the industry. This in-depth exploration will unravel the potential implications of 1-second transaction finality for user experience, network scalability, and overall performance in the Harmony network, setting the stage for the upcoming sections of this paper.

Background and Overview of Harmony Protocol

Harmony Protocol is a cutting-edge blockchain network implementing deep sharding and novel consensus mechanisms. Utilizing sharding technology at the state, network, and transaction level, Harmony aims to overcome one of the most significant challenges in the blockchain space: scalability with security. Coupled with a consensus mechanism known as Effective Proof-of-Stake (EPoS), Harmony provides a solution for the trilemma in the blockchain space, efficiently balancing decentralization, security, and scalability.

Sharding in Harmony Protocol

Sharding technology forms the backbone of Harmony’s scalable architecture. “Sharding” refers to dividing a larger set of nodes into smaller sets, or “shards”, each capable of parallel processing transactions and smart contracts. This is analogous to splitting a larger database into smaller, more manageable parts, each operating independently in harmony.

Mathematically, we denote the number of shards as S, where each shard comprises n nodes. Therefore, the total number of nodes in the network, N, can be expressed as N = S ⋅ n. The critical advantage of sharding is its potential for linear scaling; as the network grows (i.e., N increases), the number of shards (S) can also increase, leading to more parallel processing and higher throughput.

Effective Proof-of-Stake (EPoS)

The bedrock of Harmony’s consensus mechanism, the Effective Proof-of-Stake (EPoS), actively counters the typical centralizing propensities ordinary in orthodox Proof-of-Stake systems. By implementing a staking threshold, EPoS limits the sway of wealthier nodes, thereby capping a node’s voting shares at a dynamic limit dictated by the median stake.

Within this context, the individual node’s stake is expressed as s_i and the median stake as s_median. The calculation for the effective stake, s_e(i), unfolds as follows:

The introduction of the logarithmic component within the latter equation guarantees that the effective stake does not escalate in direct proportion to the actual stake. This formula fosters a more equitable and balanced staking mechanism.

Fast Byzantine Fault Tolerance (FBFT)

The Fast Byzantine Fault Tolerance (FBFT) consensus algorithm is pivotal in Harmony’s 2-second transaction finality. FBFT is an optimized version of the Practical Byzantine Fault Tolerance (PBFT) algorithm, designed to deliver faster consensus by reducing the number of communication rounds.

In PBFT, three phases of communication are required (Pre-Prepare, Prepare, and Commit), each requiring n round-trip messages, where n is the number of validator nodes. However, FBFT optimizes this process by piggybacking the Prepare and Commit phases, reducing the communication complexity from O(n²) to O(n), achieving faster transaction finality.

The time for transaction finality F can be given by the equation mentioned in the introduction, F = n ⋅ t. By reducing n through the FBFT, Harmony effectively achieved 2-second transaction finality.

As Harmony continues to optimize its infrastructure, it is crucial to understand these fundamental building blocks to appreciate the engineering feat of a 1-second transaction finality. The upcoming sections will discuss how these elements interplay with Harmony’s transition to this unprecedented fast finality.

Proposed Shift to 1-second Finality

Harmony Protocol, leveraging its innovative technology stack, proposes an ambitious transition from the current 2-second finality to 1-second finality. This significant stride promises to optimize transaction speeds further, improving user experience and elevating Harmony’s competitive edge in the high-stake race of blockchain scalability.

Description of the Proposal

In pursuit of 1-second finality, Harmony presented the Harmony Improvement Proposal 30 (HIP-30). The HIP-30 aims to reduce the number of nodes in Shard 1 from 250 to 200 and accelerate development towards this goal. The key idea is to optimize consensus latency by minimizing the number of communication rounds needed between nodes. This strategy plays a critical role in achieving 1-second finality.

The original proposal suggested distinguishing between Shard 0 and Shard 1, with 250 nodes maintained on Shard 0 and 200 nodes hosted on Shard 1. This approach aimed to facilitate dynamic, live experiments without jeopardizing network stability. However, on careful reflection, it becomes clear that imposing a difference in the number of nodes between shards might complicate the sharding design unduly. To uphold the integrity and simplicity of the sharding architecture, it is advisable to maintain uniformity among shards regarding node count. Diverging from this could introduce unforeseen complications and problems; hence, uniformity across shards is strongly recommended.

Technological and Mathematical Changes

Achieving a 1-second block finality in Harmony involves a series of critical technological and mathematical adaptations. Chief among these is the need to curtail consensus latency significantly. We can achieve this by fine-tuning the Fast Byzantine Fault Tolerance (FBFT) algorithm to decrease the communication rounds required for transaction validation.

Traditionally, FBFT’s time complexity is encapsulated by the equation T = k ⋅ n ⋅ t. In this expression, T signifies the total time taken for consensus, k denotes the number of communication rounds, n represents the number of nodes, and t is the average latency per node. However, this model assumes sequential communication between the leader and validators, which is not always the practice case.

In a scenario where communication happens in parallel and block write times to local databases are a factor, a more representative model could be expressed as T = k ⋅ max(t, db), where db denotes the time to write a block to the local database.

To halve the total consensus time, T, for Harmony — the essence of 1-second finality — we need T_new = T/2. Consequently, this necessitates strategic optimization of k, t, and db. For instance, under the HIP-30 proposal, Harmony plans to reduce n from 250 to 200. A 20% reduction in the number of nodes could potentially lead to a comparable decrease in consensus time, edging Harmony closer to its target 1-second finality.

Next, reducing nodes per shard also means a decrease in BLS keys per validator. This necessitates a well-crafted strategy to distribute the BLS keys equitably, maintaining the unique balance of Harmony’s Effective Proof-of-Stake (EPoS) model.

Moreover, as we shift towards 1-second finality, upholding the integrity of cross-shard communications becomes paramount. With shards processing transactions in parallel, stringent coordination and synchronization between shards is essential to prevent double-spending and ensure overall consistency.

Harmony’s ambitious stride towards 1-second finality underpins its dedication to pushing the envelope of blockchain technology, heralding a new epoch of highly efficient, scalable networks. The following sections will probe deeper into the potential ramifications of this transition for Harmony Protocol and the broader blockchain ecosystem.

Comparative Analysis

A comprehensive comparative analysis offers valuable insights into the implications and potential outcomes of transitioning to a 1-second finality on the Harmony Protocol. The comparison focuses on qualitative and quantitative aspects, providing a holistic perspective on this significant shift.

Detailed Comparison between Current and Proposed Finality Times

Harmony currently operates with a 2-second finality time, already an exceptional achievement in the blockchain ecosystem. This speed is made possible by the protocol’s innovative sharding and EPoS design and utilizing FBFT for consensus. However, the move to 1-second finality promises further to amplify the network’s efficiency and user experience.

The current 2-second finality is characterized by the equation T = k ⋅ n ⋅ twith n = 250 nodes in Shard 1. Reducing n to 200 in the proposed scenario leads to a 20% reduction in the consensus time, bringing it closer to the 1-second target.

Potential Improvements and Drawbacks of 1-second Finality

The leap to 1-second finality bears significant advantages. Foremost among these is the drastic user experience enhancement facilitated by near-immediate transaction confirmations. This increase in speed paves the way for highly responsive and scalable decentralized applications (dApps), especially in the burgeoning DeFi sector, bolstering Harmony’s appeal to developers.

Further, the shorter finality time could spur a surge in transaction volume, thus amplifying network throughput. Theoretically, this change could double Harmony’s transaction processing capacity per time unit.

Nevertheless, transitioning to 1-second finality has potential challenges. For one, the reduction in node quantity may have implications for network resilience against Byzantine behavior. Accelerated consensus could also demand more from node hardware, raising the entry bar for some validators.

Moreover, the increase in block generation associated with a faster finality time is anticipated to accelerate the growth of storage space requirements. This aspect necessitates careful consideration and planning to ensure it is a manageable factor in the network’s scalability.

Quantitative Comparison of Potential Transaction Volume, Security Implications, and Other Key Metrics

Regarding security, the decreased number of nodes per shard could marginally lower resilience against Byzantine nodes. The mathematical relation f < n/3 defines the fault tolerance threshold in a Byzantine fault-tolerant system, where f is the maximum number of Byzantine nodes the system can tolerate, and n is the total number of nodes. The theoretical resilience is marginally lowered with n reducing from 250 to 200. However, Harmony’s EPoS model can mitigate this to a great extent.

The management of finality time reduction needs to be approached with precision to circumvent a rise in the rate of orphan blocks, as this could detract from network efficiency. To elaborate, orphan blocks or “stale blocks” are valid blocks that do not make it into the main blockchain, often due to simultaneous block production by miners or lag in network propagation. A high rate of these orphan blocks suggests an inefficient usage of resources since computational power is allocated to blocks that do not lengthen the chain. In a quantitative context, if we let r represent the block production rate and d symbolize network delay, it is vital to ensure r < d to keep orphan rates at bay.

The transition to a 1-second finality offers impressive potential improvements but demands meticulous design and implementation to manage potential drawbacks. The succeeding sections will examine the practical considerations of implementing this transition and the potential future Harmony Protocol developments.

Mathematical Modeling of 1-second Finality

Mathematical modeling provides the logical structure that underpins the feasibility and implications of transitioning to a 1-second finality. By representing the elements of the Harmony system and their interactions through mathematical equations, we can predict system behavior under various conditions, offering valuable insights into the potential dynamics of the proposed changes.

Introduction to the Models and Equations Used in the Paper

This paper utilizes several mathematical models to analyze and predict the behavior of the Harmony system under the proposed changes.

Consensus Time Model: The consensus time (T) in Harmony is approximated as T = k ⋅ n ⋅ t, where k is a constant, n is the number of nodes, and t is the time taken for a single communication round. Reducing n from 250 to 200 would lead to a direct reduction in consensus time.

Fault Tolerance Model: The fault tolerance threshold f in a Byzantine fault-tolerant system is defined by f < n/3. Reducing the number of nodes (n) from 250 to 200 marginally lowers the theoretical resilience.

Orphan Block Rate Model: If r is the block production rate and d is the network delay, maintaining r < d is essential to prevent high orphan rates.

Detailed Discussion of the Mathematical Modeling of the Proposed System

Our mathematical modeling represents the interactions within the Harmony system, considering the parameters and variables that influence transaction finality time, throughput, security, and efficiency.

In the Consensus Time Model, by decreasing n from 250 to 200, there is an immediate reduction in the consensus time — a significant step towards achieving the 1-second finality.

The Transaction Throughput Model predicts that with the finality time halved, the transaction throughput should theoretically double, implying that Harmony could process twice the current volume of transactions per second.

The Fault Tolerance Model suggests a marginal decrease in the network’s tolerance to Byzantine nodes. However, this potential drawback is mitigated by Harmony’s EPoS model, which punishes malicious validators by slashing their stakes.

Lastly, the Orphan Block Rate Model alerts us to the potential risk of an increased orphan block rate if the transition to 1-second finality is not appropriately managed. Reducing the finality time without appropriate adjustments to the network delay could result in a higher orphan rate, reducing the network’s overall efficiency.

Analysis of the Model Results and Their Implications

The model results illuminate the potential for impressive improvements and possible challenges that the transition to 1-second finality may bring.

The consensus time and transaction throughput models indicate a notable performance enhancement in transaction speed and volume, promising a vastly improved user experience and a more competitive protocol for DeFi applications.

Meanwhile, the fault tolerance and orphan block rate models highlight the need for meticulous design and implementation in the transition to prevent potential drawbacks, particularly concerning security and efficiency. Despite the reduced resilience against Byzantine nodes, Harmony’s EPoS model safeguards against malicious activities, ensuring the network’s robustness.

Conclusively, these models present a comprehensive overview of the network’s potential performance under 1-second finality, guiding the design and implementation process. The following section will delve into the practical considerations of executing this transition.

Responsiveness in Blockchain Protocols

The concept of responsiveness within blockchain protocols significantly enhances such systems’ performance, scalability, and efficiency. It refers to a protocol’s capability to adapt to real-world network conditions and function optimally within the network latency rather than being constrained by a predetermined, hardcoded delay limit, denoted as Δ.

In essence, responsiveness manifests as the protocol’s capability to progress within the “real network delay,” denoted as δ. This actual network delay is typically less than or equal to Δ and represents the time it takes for information to propagate through the network.

In practice, the responsiveness of a blockchain protocol has profound implications for its speed, performance, and user experience. A responsive protocol adjusts its operation to real-time network conditions, allowing it to achieve faster transaction confirmations during periods of low network latency. It ensures that the protocol functions at its maximum potential and is not limited by a maximum delay set during its design phase.

Therefore, The principle of responsiveness becomes pivotal when designing protocols that aim for high-speed transaction confirmations, such as Harmony’s proposed 1-second finality. By implementing a responsive design, Harmony can make significant strides in its quest for rapid finality without jeopardizing the security and reliability of the network. In the following subsections, we will delve deeper into this concept by examining some recently proposed responsive consensus protocols and exploring how their techniques might be incorporated into Harmony’s design.

Review of PaLa and Simplex Consensus Protocols

The concept of responsiveness in blockchain protocols is an active area of research, with numerous contributions being made in the recent past. Two notable contributions include the PaLa: A Simple Partially Synchronous Blockchain and Simplex Consensus: A Simple and Fast Consensus Protocol papers.

PaLa: A Simple Partially Synchronous Blockchain

The PaLa paper proposes a new protocol named PaLa, which operates under a partially synchronous network model. It is a simple protocol that combines ideas from Tendermint and HotStuff while aiming for high responsiveness. The protocol assumes a partially synchronous model with a known upper bound Δ on message delay, but the actual delay δ is unknown. The protocol guarantees that if the network delay is less than Δ, then the protocol completes in roughly 2δ time.

PaLa is designed to achieve two key goals. The first is safety, where the protocol guarantees that no two honest validators commit different blocks at the same height. The second is liveness, where every honest validator eventually commits some block at every height. PaLa achieves these goals by carefully structuring the voting process involving two voting steps: prevote and precommit. In essence, a validator must witness more than 2/3 of validators prevoting a block to precommit it and more than 2/3 of validators precommitting a block to commit it.

Simplex Consensus: A Simple and Fast Consensus Protocol

The Simplex Consensus study presents an innovative consensus protocol that, while maintaining the integrity of safety and liveness, streamlines the consensus process with a unique approach to consensus rounds and voting. Named Simplex, this protocol ensures network robustness more effectively and efficiently than the predecessor, PaLa.

Each round in Simplex comprises three key phases: Proposal, Soft vote, and Certify. Initially, an honest validator suggests a block during the Proposal phase. This is followed by the Soft vote phase, where the validator waits to gather a requisite number of soft votes. Lastly, the Certify phase involves gathering sufficient certifications to endorse and confirm a block.

A key feature of Simplex lies in its progressive approach within the actual network delay δ, which trumps the traditional method within the worst-case upper-bound Δ. This allows the protocol to achieve responsiveness. Moreover, Simplex introduces a pioneering mechanism that authorizes validators to securely transition to the next round when the present round seems stagnant, thereby enhancing overall efficiency.

The strategies to actualize responsiveness in the Simplex protocol involve meticulously structured voting mechanisms and transitions between rounds. Validators make choices based on the input from a supermajority of other validators. This way, the protocol’s progress is intimately linked to the actual network delay instead of a pessimistic estimate. Such approaches are crucial when optimizing transaction finality times, especially in protocols like Harmony.

Potential Implementation in Harmony Protocol

The methodologies from both PaLa and Simplex protocols offer intriguing possibilities for Harmony Protocol in its quest for achieving a 1-second finality. Adapting these techniques, Harmony can redesign its consensus algorithm to be responsive, offering increased performance.

Implementation Considerations

First, Harmony’s current use of FBFT can be enhanced by incorporating some principles from PaLa and Simplex protocols. The voting mechanism in PaLa, which involves two steps — prevote and precommit — could provide a blueprint. Similarly, the Proposal, Soft vote, and Certify phases from Simplex could be implemented within the FBFT algorithm. However, this would require careful redesign to avoid creating new vulnerabilities or disrupting existing efficiencies.

The quest for improved performance in the Harmony protocol, particularly during periods of high transactional load or spam attacks, is not without its hurdles. One such challenge is the time it takes to insert a block into the local database — a process that has historically constituted a notable system bottleneck. However, the solution we once implemented, a local sharding database strategy, did not result in sufficient performance gains to justify its operational overhead, especially when faced with a full disk.

This approach, which involved data splitting across different disks to distribute the load and decrease insertion time, brought about performance improvements of only 10–20%. Although available, this feature currently needs to be used due to its inadequate efficiency-cost trade-off.

However, it is worth mentioning that obstacles like these can provide valuable insights into the network’s operational efficiency. This specific challenge and others guide our ongoing exploration of strategies like implementing a responsive consensus algorithm (such as PaLa or Simplex). As we persist in this endeavor, we inch closer to Harmony’s aspiration of realizing 1-second finality and amplifying our transaction processing capability twofold.

While both protocols operate under the assumption of a partially synchronous model, Harmony must identify the most suitable delay bounds for its network. It must also redesign its slot allocation and leader selection mechanisms to align with the updated consensus protocol.

Potential Benefits and Drawbacks

The primary benefit of adopting the responsive consensus approach is the potential to achieve a faster block finality time — possibly reaching the desired 1-second finality. This could drastically improve transaction throughput and overall network performance.

Additionally, in the context of Harmony’s Effective Proof-of-Stake (EPoS) and shard chains, responsiveness might enhance the robustness of the consensus algorithm. A protocol that can adjust to actual network delays could better handle fluctuations in network conditions, thereby maintaining high levels of performance and reliability.

Transitioning to a responsive protocol poses challenges. This would require an extensive redesign of Harmony’s consensus mechanism. Any changes to this critical aspect of the network should be cautious to avoid new security vulnerabilities or unintended consequences. Theoretical benefits must be empirically validated.

Incorporating the strategies from PaLa and Simplex into Harmony Protocol could catalyze significant enhancements in transaction finality speed. However, such an integration warrants rigorous exploration and a comprehensive understanding of its potential impacts before application. Despite the potential advantages, the necessity of these implementations comes into question considering empirical evidence from the Harmony network. Historical data indicates that shards 1, 2, and 3 successfully managed 1-second finality without any need for node reduction in the past. Thus, Harmony could attain its objective of 1-second finality without necessitating the full adoption of PaLa and Simplex, underscoring the importance of this research line in Harmony’s ongoing evolution.

Further Investigation into Responsive Protocols

The promising results of incorporating responsiveness in consensus protocols, as evidenced by PaLa and Simplex, warrant deeper investigation. Further exploration into the mechanisms underlying these protocols and a comprehensive understanding of their strengths and weaknesses will provide the foundation necessary for the proposed adaptation.

Modifying the Harmony Codebase for Reduced Block Time

As Harmony aims to optimize its network for faster transaction finality, it is crucial to delve into the codebase to understand where key parameters governing block times are set and how they can be adapted. This exploration is a fundamental step toward transforming the theoretical foundations of PaLa and Simplex into practical implementations on the Harmony network.

In Harmony’s codebase, specifically within the consensus_service.go file, one can locate the BlockPeriod field in the consensus object. This field indicates the time interval between consecutive block generations.

consensus.BlockPeriod = 5 * time.Second

This line sets the block period to five seconds. However, a conditional statement later adjusts this interval for certain epochs.

// Enable 2s block time at the twoSecondsEpoch
if consensus.Blockchain().Config().IsTwoSeconds(nextEpoch) {
  consensus.BlockPeriod = 2 * time.Second
}

This conditional checks whether the next epoch is configured for two-second blocks and, if so, changes the BlockPeriod to two seconds.

While this approach provides a straightforward way to manage the block time, it inherently restricts the system’s flexibility. Any adjustments to the block time currently necessitate code changes and subsequent deployment across the network.

To drive Harmony toward achieving a 1-second block time, the block time setting in the codebase must be carefully revised. This requires a comprehensive mathematical model and rigorous testing to validate the robustness of the network under the proposed changes. One potential modification could be to introduce a condition for one-second block periods.

// Enable 1s block time at the oneSecondEpoch
if consensus.Blockchain().Config().IsOneSecond(nextEpoch) {
  consensus.BlockPeriod = 1 * time.Second
}

This modification suggests a conditional epoch where one-second block periods become active. However, such a transition must be cautiously implemented, as shorter block times could introduce additional strain on the network. Challenges such as increased load, network congestion, and a potential rise in orphaned blocks must be addressed during this transition. Ensuring the network’s stability and performance under these circumstances will be critical in Harmony’s journey toward 1-second finality.

Implications for Blockchain Technology

The advent of 1-second finality in the Harmony protocol is set to reverberate throughout the blockchain ecosystem. While it is a significant milestone for Harmony itself, the ripple effects will likely inspire a wave of advancements in blockchain technology.

First and foremost, the possibility of 1-second finality would serve as a beacon for scalability in the blockchain ecosystem. With this achievement, Harmony would double its transaction throughput, thereby substantially increasing the potential transaction volume that can be handled per unit of time. This dramatic improvement in scalability would be a boon for decentralized applications, particularly in the DeFi sector, where transaction speed and volume are critical.

The impact on security, while nuanced, is also worth noting. Though fewer nodes might marginally decrease the network’s theoretical fault tolerance, implementing this transition with Harmony’s robust EPoS model safeguards against malicious activities. Therefore, this model can serve as a blueprint for other blockchain networks looking to enhance their performance while maintaining high-security standards.

Decentralization, a core tenet of blockchain technology, would not be compromised under this transition. The number of nodes would still be substantial to ensure a decentralized network and the democratic ethos of the Harmony ecosystem would continue to thrive.

Conclusion

The adoption of 1-second finality, as detailed in this paper, signifies a landmark moment for Harmony and the broader landscape of blockchain technology. Our mathematical models indicate a significant increase in transaction speed and capacity, alluding to a superior user experience and an enhanced protocol well-suited for high-volume applications, particularly in the sphere of DeFi.

Despite the potential benefits, the journey to 1-second finality requires careful management to address potential security and efficiency implications. Our mathematical analysis shows that reducing the number of nodes could slightly lower the network’s resilience to Byzantine behaviors. However, the protection offered by Harmony’s EPoS model against such adversarial actions emphasizes the network’s robustness.

This study paves the way for future research in various domains. For example, a deeper evaluation of the EPoS model under the newly proposed conditions is warranted. Further, a comprehensive exploration of 1-second finality’s impact on factors such as network latency, computational overhead, and resource utilization could yield significant insights. Lastly, empirical testing and evaluation of the proposed system will provide practical data to corroborate our theoretical conclusions.

As explored in this paper, the progression toward 1-second finality within the Harmony protocol holds immense potential. It exemplifies Harmony’s dedication to ongoing advancement and innovation, continually redefining the limits of what is feasible in the blockchain ecosystem.